Les maths clés en main avec Totem (CP, CE1, CE2)
Une méthode de mathématiques explicite et très guidée, rassurante pour l’élève avec un apprentissage progressif et spiralaire des notions.
Points forts
Les points forts de la méthode Totem au cycle 2 :
- Une progression adaptée et spiralaire.
- Une programmation annuelle clé en main.
- Une pédagogie explicite assurant une progression pas à pas vers l’abstraction, la compréhension, l’automatisation, la mémorisation, l’autonomie.
- Une méthode rassurante pour les élèves avec des exercices récurrents et des leçons claires.
- Une attention particulière aux élèves fragiles pour anticiper les erreurs et apporter les aides méthodologiques.
- Un enseignement inédit en géométrie : gestes de base pour apprendre à travailler avec précision.
- De larges temps de manipulation au CP.
Démarche
Présentation de la méthode
Une organisation par domaines :
Numération : des activités très ritualisées pour un apprentissage spiralaire de la construction du nombre.
Calcul posé : une modélisation des différentes étapes des techniques de calculs.
Résolution de problèmes : l’acquisition d’une méthodologie pérenne. Enseignement par la manipulation puis par le calcul et par l’analyse de l’énoncé et la forme de réponse attendue.
Calcul mental : la mémorisation des faits numériques et le calcul automatisé sont entrainés quotidiennement du CP au CE2 pour installer les savoir-faire nécessaires au calcul réfléchi abordé au CE2.
Géométrie : un enseignement extrêmement guidé et précis (vidéos) pour apprendre les bons gestes.
Grandeurs et mesures : l’étude des grandeurs fait la part belle à la manipulation et entraine l’acquisition des unités de mesures.
Pour un enseignement efficace, les auteurs préconisent :
La progressivité, explicitation et entrainement
Une approche pas-à-pas avec des apprentissages distincts et segmentés, des objectifs intermédiaires, et un étalement dans le temps avec une pédagogie qui énonce clairement à l’élève tout ce qui lui sera demandé de savoir et de savoir-faire.
Les savoirs et savoir-faire enseignés doivent être compris mais aussi entrainés au travers d’activités mathématiques programmées et de nombreuses répétitions.
La méthodologie, un axe fort de l’enseignement des mathématiques
Note des auteurs
Nous faisons le pari que les programmes peuvent être menés à bien tout en y insérant un enseignement méthodologique, prenant appui sur des modèles, des exemples et un accompagnement individuel. Nul doute que l’élève en tirera profit dans l’immédiat mais plus encore à long terme.
Un enseignement précis pour des apprentissages sur le long terme
Afin d’éviter chez certains élèves une maitrise insuffisante de savoirs ou de savoir-faire de base, qui fait obstacle à des acquisitions de plus haut niveau, les auteurs préconisent un enseignement précis, par exemple : veiller à ne jamais écrire ≪ 48 + 12 = … ≫ au tableau ou sur une fiche d’exercices pour formuler une consigne qui est, en réalité : ≪ Calcule 48 + 12. ≫.
La manipulation, un passage obligé mais seulement une étape de l’apprentissage
Note des auteurs
Notre enseignement des mathématiques au CP doit prendre en compte ce besoin de manipuler pour permettre au plus grand nombre d’accéder aux compétences visées, mais sans perdre de vue le but à atteindre : le raisonnement dans l’abstraction. Par conséquent, il n’est pas inutile de préciser que les activités de manipulation sont préparatoires aux mathématiques et pas réellement des mathématiques. Cela permet notamment de ne pas se tromper sur leur portée réelle.
Témoignages d’enseignants utilisateurs
Première année d'utilisation de Totem CP. Je suis convaincue de l'efficacité de cette méthode et l'utiliserai donc dès la rentrée prochaine en cours double : CP-CE1. Tout est explicite pour l'enseignant et rassurant pour l'élève. Le cahier journal de l'enseignant est un parfait guide du maître, détaillant au jour le jour chaque séance. Le mémo est un outil précieux pour l'élève ; on y retrouve les référentiels ainsi que les traces écrites. Les cinq domaines sont entièrement et progressivement balayés : numération, calcul mental et posé, résolution de problèmes, géométrie ainsi que grandeurs et mesures. Un emploi du temps est proposé permettant ainsi une programmation réussie. Les apprentissages sont progressifs et prennent en compte tous les besoins des élèves via des activités très ritualisées (travail quotidien sur la comptine numérique par exemple), de la manipulation, des fiches activités, le début de la mémorisation de faits numériques, l'utilisation des instruments en géométrie, la résolution de problèmes ... Les élèves progressent et sont rassurés car la méthode est progressive et très explicite.
Les outils
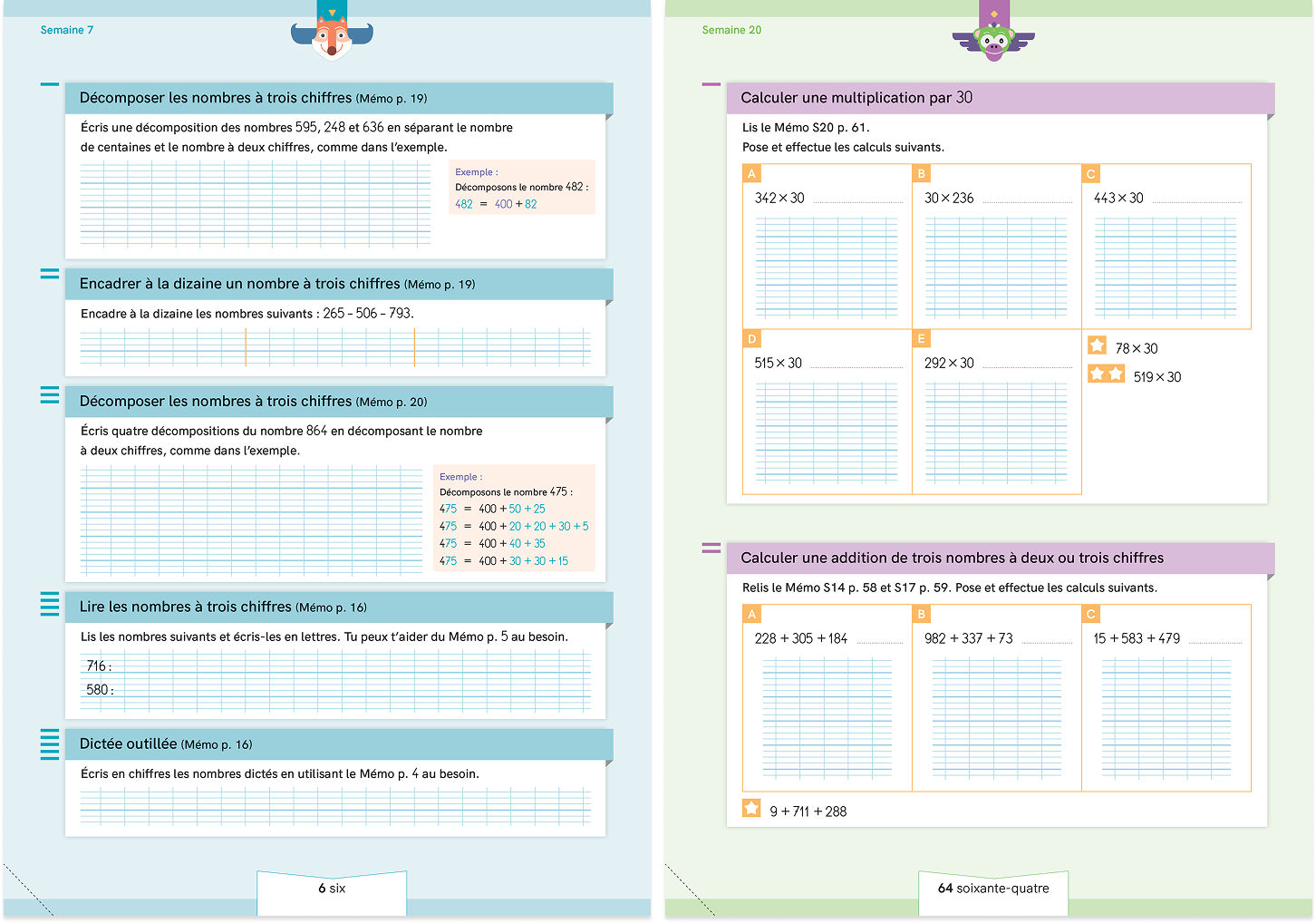
Les fichiers de l’élève
Deux fichiers d’exercices par niveau, dans lesquels l’élève se repère facilement :
- des planches prédécoupées pour s’entrainer à mémoriser des calculs et manipuler la monnaie
- 1 feuille de calque
Ils sont sans perturbateurs visuels et présentent des consignes récurrentes pour s’entrainer toute l’année et installer durablement les savoir-faire.
Extrait du fichier Nombres et calculs CE2
Le mémo de leçons
Référentiel simple et visuel des leçons de l’année, il est adapté aux jeunes lecteurs et destiné à une utilisation fréquente et durable pour retrouver les savoirs et savoir-faire appris ou à apprendre. Des leçons très explicites, guidées pas à pas et toujours illustrées d’un exemple, organisées par domaines. Le Mémo de leçons permet à l’élève de relire les leçons à l’école ou à la maison et de stabiliser ses apprentissages.
Bon à savoir
Le cahier-journal de l’enseignant
Le guide pédagogique exhaustif et détaillé (progression, activités collectives, de manipulation…) avec des ressources numériques à télécharger dont les diaporamas qui explicitent les méthodologies.
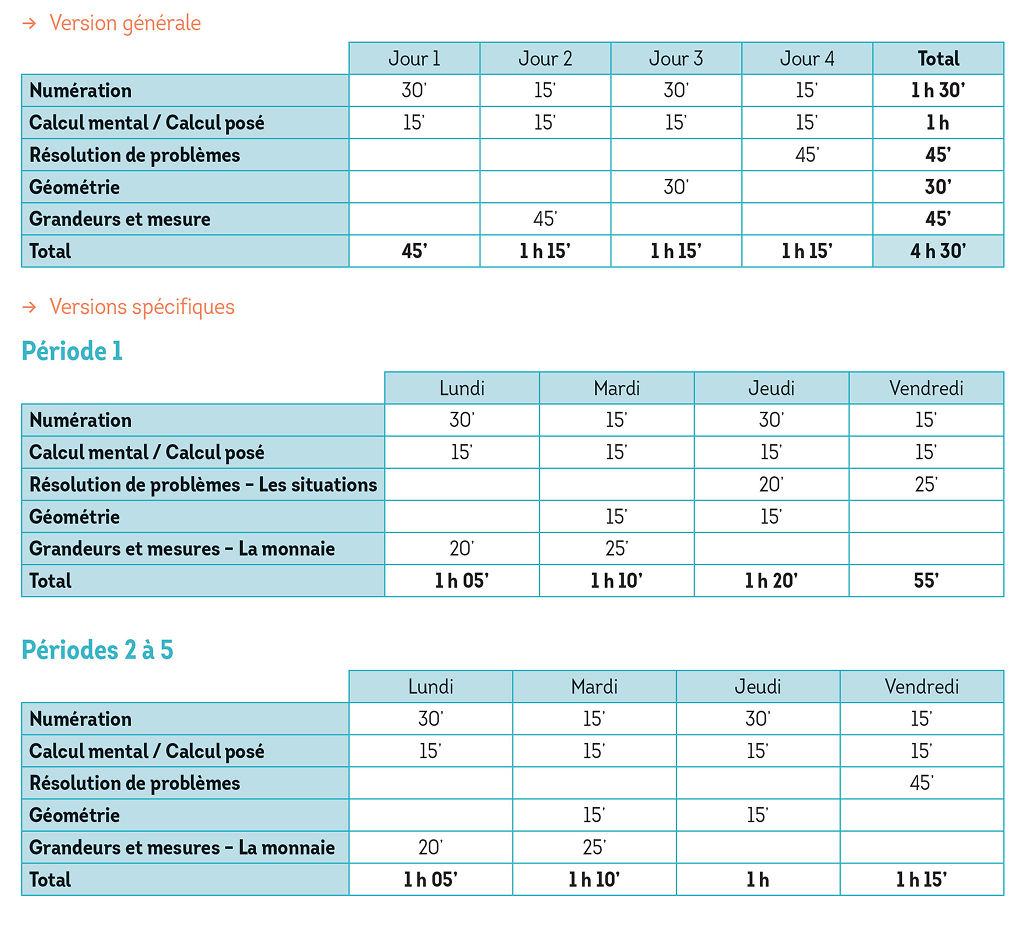
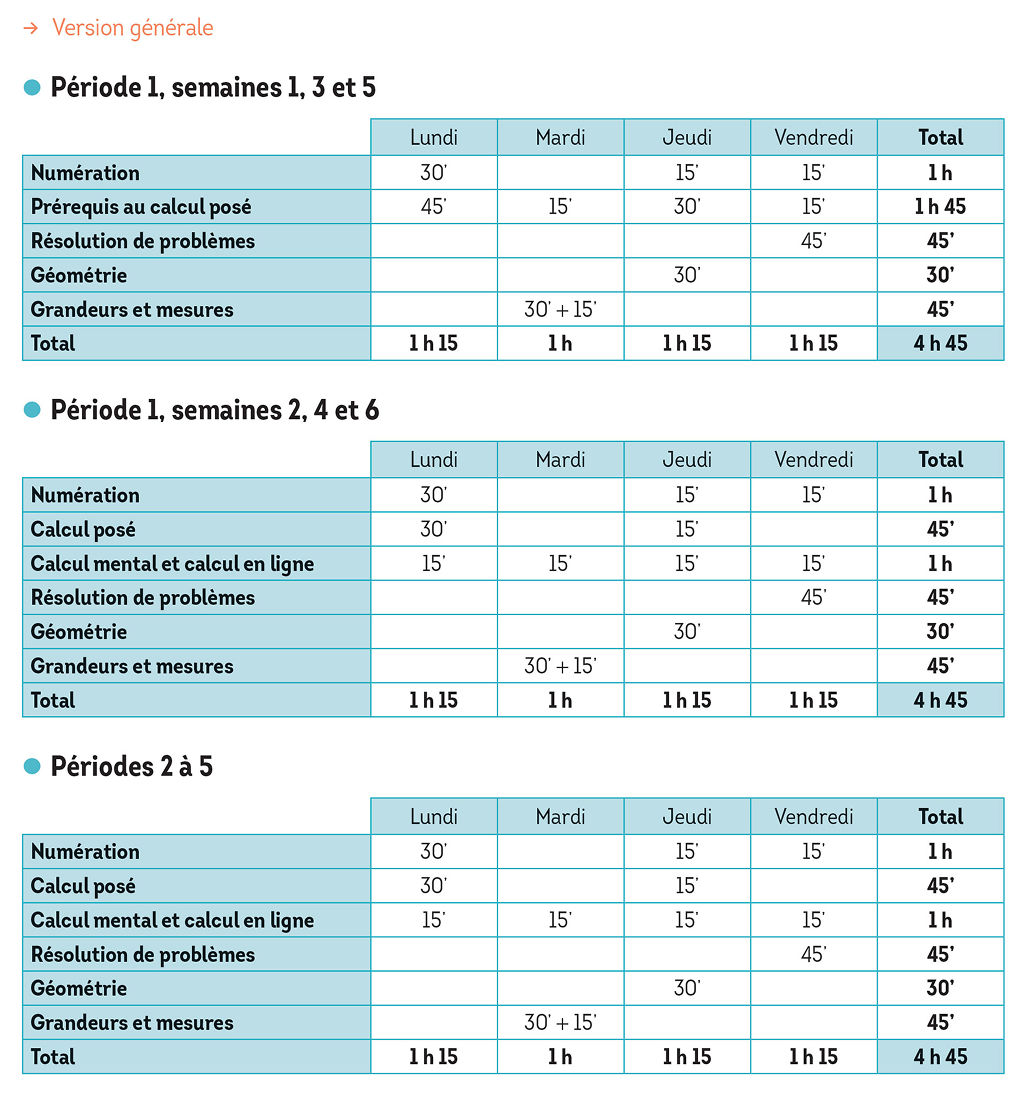
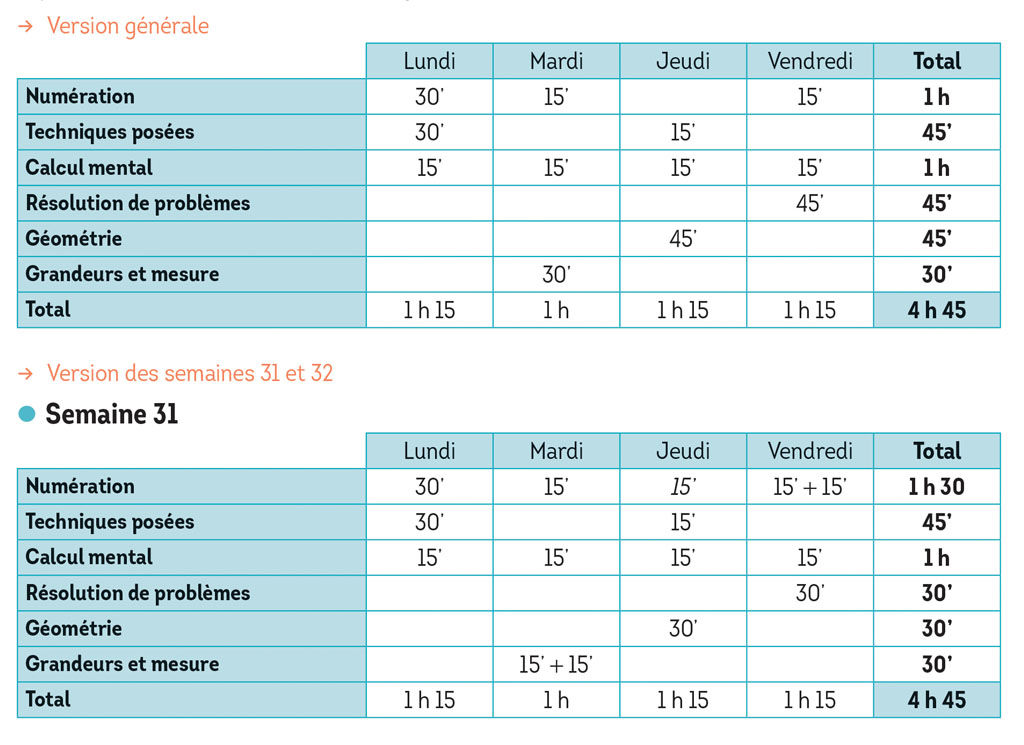
La programmation
Les auteurs recommandent une répartition hebdomadaire des séances de mathématiques avec Totem, car cette organisation garantit la régularité et la continuité des apprentissages au sein de chaque domaine.
Bon à savoirLa programmation
par semaine au CP
La programmation
par semaine au CE1
La programmation
par semaine au CE2
Les séances
Elles sont brèves le plus souvent (15 minutes). Dans le cas contraire, elles sont composées de plusieurs activités distinctes (durée de 30 à 45 minutes).
Note des auteurs
On le sait, l’attention de l’élève doit être optimale pour garantir l’efficacité de l’enseignement, en particulier lors des phases collectives. De plus, la qualité du travail individuel est d’autant meilleure que celui-ci est court, plus particulièrement lorsqu’il est écrit.
Dans plusieurs domaines, des activités reviennent à l’identique plusieurs périodes durant, avec une variation d’un paramètre, en général le nombre. C’est par exemple le cas de la mémorisation de faits numériques en calcul. Ces activités sont alors détaillées dans les « fiches activités » au début de chaque domaine dans le cahier journal de l’enseignant.
Extrait du guide pédagogique Totem CE1
Lorsque la séance est destinée à enseigner un savoir-faire, elle présente 3 étapes :
- Le savoir-faire est présenté avec un ou plusieurs exemples qui constituent un modèle de sa mise en œuvre.
- Suivent des exemples traités collectivement
- Un travail individuel permet à l’élève de s’entrainer et à l’enseignant de faire le point.
Enfin certaines séances, notamment dans le domaine des mesures, sont destinées à faire expérimenter les élèves. Les manipulations utiles en constituent alors l’essentiel de la durée.
Bon à savoirPar exemple, comment se passe une semaine avec Totem CE2 ?
Les supports visuels : vidéos, diaporamas pour renforcer la compréhension et la mémorisation
Des vidéos d’aide à la géométrie
Des vidéos sont proposées sur le site compagnon pour le domaine Espaces et géométrie.
Ces courtes vidéos permettent à chaque élève de mieux visualiser et d’intégrer les bons gestes.
L’activité individuelle qui suit sert d’entrainement, ce qui implique la répétition du ou des gestes travaillés, sans aller jusqu’à la lassitude et la déconcentration qui en découlent.
De nombreux affichages collectifs – diaporamas
Des affichages collectifs / diaporamas sont proposés sur le site compagnon pour introduire les savoir-faire à travers des modèles clairs et des exemples collectifs tout au long de l’utilisation de la méthode.
Le recours à ces supports visuels permet d’accompagner les traces écrites des savoir-faire.
Programmes 2025
Totem CP est conforme aux programmes 2025.
Pour Totem CE1, des séances sur les fractions seront disponibles sur le site compagnon (été 2025).
Totem CE2 propose des leçons et des activités pour travailler les points essentiels des programmes 2025 :
- Connaitre et utiliser les nombres jusqu’à 10 000 (composer, décomposer, ordonner, comparer…)
- Comprendre, lire, écrire, comparer les fractions d’un tout et d’une unité
- Maitriser les 4 opérations
- Mémoriser les faits numériques et utiliser des stratégies de calcul mental
- Comprendre, modéliser, calculer et répondre à des problèmes variés
- Connaitre et utiliser les différentes unités de mesure
- Utiliser l’écriture à virgule pour la monnaie
- Connaitre le vocabulaire de géométrie, savoir reproduire des figures et les coder…
- Savoir prélever des informations dans des graphiques
CE2 : focus sur 3 points des programmes 2025
Numération
Fractions : 5 leçons et 16 exercices pour comprendre, lire, écrire et comparer les fractions
Résolution de problèmes
Histogrammes : une leçon et 3 exercices pour s’entrainer à la lecture et à la réalisation de diagrammes en barres
Monnaie
Nombre à virgules : une leçon et 4 exercices pour lire, écrire et calculer avec des nombres à virgule dans le contexte de la monnaie
Dispositif complet
Offre papier CP
Offre numérique CP
Offre papier CE1
Offre numérique CE1
Offre papier CE2
Offre numérique CE2
Matériel
- Elle convient à toute méthode d'enseignement des mathématiques : cubes unités ; cartes unités, dizaines, centaines individuelles et collectives ; jeux de loto ; cartes nombres; mètres ruban ; toises ; file numérique…
- Conçue pour 8 élèves.
Bon à savoirLes auteurs
Christian Henaff – Directeur de la collection Totem
Christian Henaff est conseiller pédagogique honoraire, de la circonscription de Tulle Vézère, circonscription rurale, dont les classes sont le plus souvent composées de cours multiples.
Affecté en Corrèze en 1994, Christian Henaff y a conduit des formations de formations initiale et continue. Par ailleurs, de 2000 à 2018, il a organisé chaque année un défi mathématique pour les élèves du CP au CM2. De 1979 à 1994, il a exercé la fonction d’instituteur adjoint dans différentes écoles élémentaires situées en « zone sensible » de la banlieue parisienne, pour les niveaux du CP au CM2. Il a également été maître d’accueil temporaire et instituteur maître formateur de 1990 à 1994.
Sandrine Peyronie
Sandrine Peyronie est conseillère pédagogique généraliste de la circonscription de Tulle Dordogne en Corrèze, circonscription rurale, dont les classes sont le plus souvent composées de cours multiples.
Affectée sur des postes de conseillère pédagogique depuis 2007 (poste ASH /EPS puis généraliste), Sandrine Peyronie a conduit des actions de formation initiale et continue. Par ailleurs, de 2010 à 2019, elle a organisé chaque année un défi mathématique pour les élèves de la GS au CM2.
De 1995 à 2007, elle a exercé en classe unique et dans les différents niveaux de la MS au CM2 (presque exclusivement en cours multiple). Elle a eu des fonctions de TRS, directrice d’école et EMF.
Isabelle Doulcet
Depuis septembre 2023, Isabelle Doulcet est conseillère pédagogique généraliste de la circonscription de Tulle Vézère en Corrèze, en milieu rural avec des classes souvent à cours multiples.
Après des débuts de carrière, en 1995, en classe unique et de nombreuses années en CM1-CM2 ; de 2013 à 2023, elle a exercé alternativement en GS-CP et CP-CE1, tout en étant directrice d’une école de 5 classes.
Patrice Millery
Patrice Millery est professeur dans une classe de CE2-CM1-CM2, en zone rurale (commune de Chanteix).
Virginie Martinie